... >>
量结果中的关系是怎样的呢?它们当中的哪些一起变化,而且变化的角度相同?只有了解数据是如何相关的,哪些测量与其它一些测量没有什么关系,他才能设计一套理想的测试来指示智力情况。
在他进行遗传天才研究时,其中的一个奇怪发现使他开始考虑到了这个问题:父母不同寻常的孩子一般不那么与众不同。比如,从生理特征上来说,父母很高的孩子倾向于不那么高,不过仍然高于平均值,而父母很矮的孩子却不那么矮,可平均还是比别人矮,这个倾向,高尔顿把它叫做“回归平常”(后来,这个词变成了“回归中间值”)。他希望知道,它在指示遗传力量上有什么意义,以及如何以数学方式表达出来。从表面上看去,这似乎就是一个纯粹的智力谜,但结果,解决这个问题的办法将成为心理学和其它许多学科当中最为有用的研究工具之一。
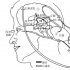
高尔顿对这个问题考虑了很长一段时间,然后对约3O0名儿童的身高确定了一个“散点方案”。首先,他画一个栅栏,横向的尺度是孩子的高度,垂直尺度为父母的身高(实际上是“中间父母”的身高——每对父母的平均身高)。然后,在每个栅栏的格子里面(特定的某个孩子的身高与某个特定的父母身高之间的交叉点),他填上符合这个条件的孩子们的人数。这张散点图的样子如下所示:
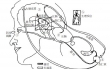
有一阵子,这个图没有给他带来任何启示;接着,一天早晨,他一边等车一边仔细看这个图,突然间,他发现了数字间的规律。如果他画一条线,将任何一组几乎相等的值连接起来,这条线将会描述出一个斜过去的椭圆,其中心点是散点图的中心点(父母和孩子的平均值)。当他这样做,并跨过椭圆画一些线条,将其极点的横点和竖点连接起来时,它们在每个垂直栏上都通过了孩子的平均身高,且在每个横排上通过了父母的平均身高值。该图形状如下所示:
这个椭圆和跨过中间的线条显示了他一直在寻找的关系。在任何给定的父母身高中(“横向正切点轨迹”),孩子的平均身高与中间值(平均值)只有父母身高平均值与中间值偏差的三分之二,换句话说,孩子们已经向中间值“回归了”三分之一。反过来说,对于任何一个孩子的身高来说(“垂直正切点的轨迹”),父母都更加接近中间值了(也就是说,异常孩子的父母没有孩子们那么异常。)高尔顿已经发现了“回归线”这个分析工具。如果孩子们的身高与父母的身高一模一样,两条回归线就会偶合;如果孩子们的身高与父母的身高没有任何关系,则回归线互彼此垂直。而事实是,这两条线相当接近,意思是,在同一情况下的两个变量之间的关系——它们的相关性——约在总量与零之间的某个地方。
那是1886年。10年之后,高尔顿的学生,后来也是他的传记作家,英国生物测定学家卡尔·皮尔逊研究出了一个计算“相关关系系数”的数学平均值——他把它叫做r,代表回归——而不需要再建立散点图。对于任何两组数据,它将会显示出一个相关关系,从1(一种完美的一对一协变关系)到0(没有任何关系),再到——l(完全相反的关系)。到今天为止,皮尔逊法一直是评估相关性的标准方法。在父母孩子的关系中,r系数为0.47(与高尔顿第一次的计算结果稍有不同):也就是说,孩子们与人口的平均值只有父母的约一半远。
高尔顿对相关性分析的发现,其重要性无论怎么强调都不能算过分。它意味着,无论什么时候,当两个变量朝同一个方向(或者向反方向)改变时,哪怕不是同一种程度,它们也都是相关的,而相关的强度会指示它们之间的关系有多大意义。关系越紧密,它是偶然性的可能性就越小,这种连接的因果关系就越强。一个变量可能是另一个变量的原因(或者是原因之一),反过来亦是一样,或者,它们也许是其它一些原因共同发生和相关的效果。在两种情况下,一种紧密的联系表明可以解释正在研究中的某个现象。在这些数字中,如果没有一个答案,至少有一些线索存在。
(哪怕是紧密的相关关系,严格来说也有可能是“以假乱真的”——即其它一些因素的人为结果。比如,在男人中间,秃头的程度与婚姻时间的长短相关——这不是因为其中的一个因素与另一个因素有什么关系,而是因为年岁与这两个因素都有关系。后来的分析技巧已经能够筛选出这些误导性的相关关系。)
心理学家乔治·米勒在评估高尔顿的发现成果的价值时写道:
协变关系是一个重要的概念,不仅对基因学和心理学是如此,而且对所有的科学探索都同样重要。科学家就是要寻找各种现象的原因;他所发现的一切都是先决条件和必然条件之间的相关关系……高尔顿的洞察力一直,而且还将继续处在现代社会及行为科学广大的伸展地带的中心,对工程师和自然科学工作


 正在提交中...
正在提交中...